Equation of Envelop for Projectile Motion

1. Basic Theory

You might know the angle for which range is maximum on level ground, namely $45^\circ$. Notice that this is independent of velocity! For those who haven’t seen this here is the little proof -

\[\begin{align*} Range (R) & = v_x \cdot time \\ R & = v\cos\theta \cdot (2v\sin\theta / g) \\ \end{align*}\]

Here we can calculate time using $S = ut + 1/2at^2$, where acceleration is $-g$, $S$ is 0 as starting and final position are the same, and $u$ is $v\sin\theta$.

\[R = \frac{v^2 \sin 2\theta}{g}\]

Clearly $\sin$ is maximum at $90^\circ$, giving $\theta = 45^\circ$

2. Intuition?

Now we alter the problem slightly. Instead of a level surface we launch the ball from a cliff. What is angle that corresponds to the maximum range when you throw the object (with velocity $v$) from a cliff ($h$ height from the surface)?

Before going any further let me comment on one certainty, it will be $\to 0^\circ$! Why you may ask. The idea is horizontal throw ($\theta = 0^\circ$) has the most horizontal velocity. The only reason why it doesn’t correspond to max range is due to time of flight. However when you introduce a cliff, every throw gets some time in the downfall. Let us for sake of all non-zero angle throws, say downfall time from cliff to ground is same. This is not correct as all the other throws (except $0^\circ$) have some non-zero downward velocity reducing time, but let us be generous to them. Apart from this, we have a constant time, all other also enjoys time taken during the parabolic arc above the cliff. Let us say all takes time corresponding to $90^\circ$, i.e maximum time of flight. The idea is even in best case total time, the ratio of time of parabolic arc above cliff and time in downhill tends to 0 for constant velocities! The reasoning being former is constant (function of velocity) whereas later increases with height of cliff. Now when we compute range, it will be $v_x \cdot \text{TotalTime}$. Total time is something very large (downhill) + something constant (time for parabolic arc and hence small). Multiplied by $v_x$ yields

\[\begin{align*} R(h) & = v_x \times (t_{parabolic \ arc} \ + \ t_{downhill}) &\\ & = v_x \times (constant \ + \ t_{downhill}) &\\ & = v\cos\theta \times constant \ + \ v\cos\theta \times t_{downhill} &\\ & = constant^\prime \ + \ v\cos\theta \times t_{downhill} \end{align*}\]

Compared to horizontal throw, $R(h) = v \times t_{downhill}$.

Clearly for sufficiently large h, or concretely large $t_{downhill}$, for every $\theta$ we will have Range for horizontal throw > Range for inclined throw. Here is the calculation if you are a bit skeptical -

\[\begin{align*} &v \times t_{downhill} > constant^\prime \ + \ v\cos\theta \times t_{downhill} \\ &v \times (1-\cos\theta) \times t_{downhill} > constant^\prime \\ &constant^{\prime\prime} \times t_{downhill} > constant^\prime \end{align*}\]

In above everything is constant, only $t_{downhill}$ depends on $h$. For large $t_{downhill}$ above inequality is trivially satisfied. Above calculation might seem elaborate but in essence what we showed is every throw gains some constant horizontal distance in its above the cliff parabolic arc. However as $v > v\cos\theta$, after some $h$ that little increment fades away, and the relative difference in velocity catches up to that initial gain. It is like 2 car racing, one with velocity $v$ and other with $v\cos\theta$ with later having a head start of say some distance $x$ (corresponding to horizontal gain in parabolic arc). It is just matter of time when faster catches it up!¹ Using same analogy one can say after sufficient height, every throw will surpass throw that is launched at higher angle to it! I.e say, $30^\circ$ after some point will surpass $60^\circ$. I don’t know how to put the intuition more concretely but there is a strong urge to claim that $\theta$, corresponding to maximum range, will decrease monotonically till $0^\circ$.

Now let us come back the original problem of actually finding the angle.

3. Angle for maximum Range - First Try

We want to find the angle $\theta$ that corresponds to maximum $x_t$, as shown in the below figure.

Range is equal to horizontal velocity times time of flight. Horizontal velocity is $vcos\theta$ and remains constant throughout the journey. Time of flight is obtained by solving $S = ut + 1/2 at^2$, subbing $vsin\theta$ for u, -h for S, -g for a and using quadratic formula we get

\[\begin{align*} t &= \frac{-vsin\theta \pm \sqrt{v^2sin^2\theta + 2gh}}{-g} \end{align*}\]

Clearly we can’t use + solution in above as that leads to negative time. Using -ve solution we find range as -

\[\begin{align*} R &= \frac{vcos\theta}{g} \left( vsin\theta + \sqrt{v^2sin^2\theta + 2gh} \right) \\ &= \frac{v^2 sin2\theta}{2g} + \frac{vcos\theta}{g}\sqrt{v^2sin^2\theta + 2gh} \\ \end{align*}\]

Notice here if we put h = 0, we get maximum range to be $\frac{v^2sin2\theta}{2g}$, which is max at $\theta = 45^\circ$.

\[\begin{align*} &= \frac{v^2sin2\theta}{2g} \left( 1 + \sqrt{1 + \frac{2gh}{v^2sin^2\theta}}\right) \\ \end{align*}\]

Assign $H$ to be $\frac{v^2}{2g}$, we get -

\[\begin{align*} R &= Hsin2\theta \left( 1 + \sqrt{1 + \frac{h}{Hsin^2\theta}}\right) \end{align*}\]

Maximizing R is same as maximizing R/H -

\[\begin{align*} \frac{R}{H} &= sin2\theta \left(1 + \sqrt{1 + \frac{h}{Hsin^2\theta}}\right) \\ &= sin2\theta \left(1 + \sqrt{1 + \alpha \csc^2\theta}\right) \end{align*}\]

Where $\alpha = h/H$. Now this is a really messy equation for a maximizing task. We will try to convert the above equation into a polynomial like equation and you will see why!

\[\begin{align*} \frac{R}{2H} &= sin\theta \sqrt{1-sin^2\theta} \left(\cdots\right) \\ \end{align*}\]

Here replace $sin\theta$ with variable t -

\[\begin{align*} \frac{R}{2H} &= t\sqrt{1-t^2}\left(1 + \sqrt{1 + \frac{\alpha}{t^2}}\right) \end{align*}\]

One can reach a similar looking equation (not exactly the same) by subbing t for $cos\theta$. This is not a polynomial equation because when you try to eliminate square roots from the above equation, you first square on both sides. Giving $y^2$, however that it not all. To remove interior square root, after first step you will move all the non-square root terms to LHS and square it. Giving a equation which has multiple coupled degrees for both t and $\frac{R}{2H}$, up to 4th degree. This is a hard equation to crack!

4. Equation of Envelop

As we just saw finding angle is not so straight forward. The calculations becomes very messy and a need of different approach arises. We will now take a bit of detour and study the overall shape of the trajectory. The reason in some vague sense is, above we are trying to tackle 2 problems at the same time. Finding maximum range and corresponding angle. If we were able to solve for optimal angle, we could just plug and get maximum range. This coupled nature might be attributed to above mess. But unlike a purely math problem we can solve the above “hard” problem by “peeking at the solution”, say by intuition or by some other method. Imagine a problem take x lines to solve. If someone lets our a characteristic of the answer or sub solution, we can incorporate that information and reduce our solution length, maybe by less thing to prove, base our proof on top it, etc. Even in the worst case you can’t magically increase the complexity of the problem! By using ideas from overall shape of envelope of trajectories, we will find maximum range standalone and then turn to optimal angle.

Let us first find the equation of our projectile. The x-coordinate is $vcos\theta \cdot t$ and y-coordinate is given by $y = vsin\theta \cdot t -1/2gt^2$. We can substitute t from x in y and get our desired equation -

\[\begin{align*} y &= vsin\theta \frac{x}{vcos\theta} - \frac{1}{2}g\frac{x^2}{v^2cos^2\theta} \\ &= (tan\theta)x - \frac{g}{2v^2cos^2\theta}x^2 \\ \end{align*}\]

Comparing it with equation of parabola, $ax^2 + bx + c = 0$ we get

\[\begin{align*} a &= \frac{-g}{2v^2cos^2\theta} \\ b &= tan\theta \\ c &= 0 \end{align*}\]

One can quickly infer x = 0 is a root for the above equation. And other root is x = -b/a, or

\[\begin{align*} -b/a &= \frac{tan\theta}{g}\cdot 2v^2cos^2\theta \\ &= \frac{v^2sin2\theta}{g}\\ \end{align*}\]

Where we used the identity, $sin2\theta = 2sin\theta cos\theta$. Now our aim is to find equation of envelope. An envelop can be thought of as the boundary across which the family of curve don’t penetrate. For example, consider family of curves given by $y = mx$ and $m \in [-1,1]$. As we can see from the diagram, lines $y = x$ and $y = -x$ act as boundary for the region that is completely covered by family of curves.

In our case $\theta$ is the parameter for family of curves. Changing the angle we get different curves, we are looking for the equation that “overlaps” them all. Following figure clearly illustrates the point

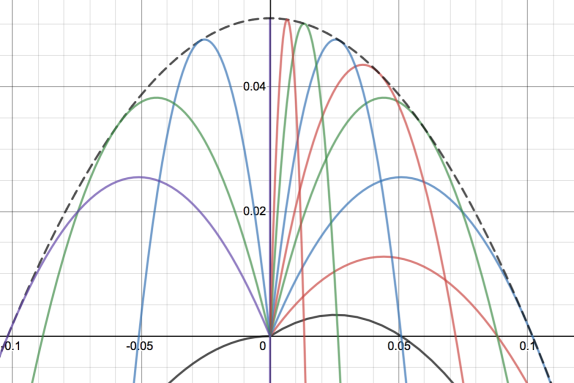Image taken from IB Maths Resources

Note that every point inside the envelope is reached by some curve! You can easily verify the claim from equation of curve. Or intuitively one can as following, at $\theta = 90^\circ$, the curve is straight up and down in a line. When we can decrease angle, the parabola base (non-zero root) moves rightwards and the utmost point moves downward. As this process doesn’t create any sudden jumps, imagine the point x,y on the plane (within the envelope). When you are decrease the angle or stretching the base, the downward motion curve sweeps the entire region! and consequently our desired point.

We can find the equation of envelope by noting that its y-coordinate is the highest y-coordinate amongst all curves (all angles). I.e imagine all curves and pick a point x on x-axis. The y-coordinate is the y-coordinate of the curve that is highest at point x.

\[\begin{align*} y &= \max_\theta \left(-\frac{g}{2v^2cos^2\theta}x^2 + (tan\theta)x\right) \\ &= x \max_\theta \left(-\frac{g}{2v^2cos^2\theta}x + tan\theta\right) \\ &= \frac{g}{2v^2}x \max_\theta \left(-\frac{x}{cos^2\theta} + \frac{2v^2}{g}tan\theta\right) \\ \end{align*}\]

As x is not a function of theta, i.e max y-coordinate of the curve is independent of x (trivial), it goes out. We can find the maxima by setting first derivative to 0.

\[\begin{align*} F(\theta) &= -x\sec^2\theta + \frac{2v^2}{g}\tan\theta \\ F^\prime(\theta) &= -2x\sec^2\theta \tan\theta + k\sec^2\theta = 0 \\ F^\prime(\theta) &= \sec^2\theta (k - 2x\tan\theta) = 0 \\ \end{align*}\]

We get either $\sec\theta = 0$ or $\tan\theta = k/2x$, where k is $2v^2/g$. We can confirm this is indeed maxima we are talking about, by looking at the second derivative. Here $F^\prime$ changes from +ve to -ve, at $0^\circ$ it is +ve as k is positive but as $\theta$ increase (tan goes from 0 to $\infty$) its turns 0 and than -ve monotonically due to monotonic nature of $\tan$. So we have $\theta^* = \tan^{-1}(k/2x)$. Substituting this $\theta$ in our equation of envelope we get -

\[\begin{align*} y &= \frac{g}{2v^2}x \left(-\frac{x}{cos^2\theta^*} + \frac{2v^2}{g}tan\theta^*\right) \\ &= \frac{g}{2v^2}x \left(-xsec^2\theta^* + \frac{2v^2}{g}tan\theta^*\right) \\ &= \frac{g}{2v^2}x \left(-x(1 + tan^2\theta^*) + \frac{2v^2}{g}tan\theta^*\right) \\ &= \frac{g}{2v^2}x \left(-x\left(1 + \frac{k^2}{4x^2}\right) + \frac{2v^2}{g}\cdot\frac{k}{2x}\right) \\ \end{align*}\]

Simplifying last equation we get

\[\boxed{y = \frac{v^2}{2g} - \frac{g}{2v^2}x^2}\]

Let $H = v^2/2g$, it is the height reached at $0^\circ$ (we can use above equation to find max height! thought angle we still need to guess). One can write above equation as $y = H - x^2/4H$. It is a parabola with roots $-2H$ and $2H$. We can use the equation of envelope to find maximum range, just plug y = -h!

\[\boxed{R_{\text{max}} = \sqrt{4H(H+h)}}\]

Now what about $\theta^*$? We will use our equation for curve (given $\theta$) and find which curve allows for above range. Put y = -h and x = $R_{\text{max}}$.

\[\begin{align*} y &= (tan\theta)x - \frac{1}{4Hcos^2\theta}x^2 \\ -h &= tan\theta\sqrt{4H(H+h)} - \frac{1}{4Hcos^2\theta}(4H(H+h)) \\ &= tan\theta\sqrt{4H(H+h)} - (1+tan^2\theta)(H+h) \\ \end{align*}\]

We get the following quadratic equation

\[\begin{align*} -tan^2\theta(H+h) + tan\theta\sqrt{4H(H+h)} - H &= 0\\ \end{align*}\]

Using formula for roots of quadratic we get

\[\begin{align*} tan\theta &= \frac{-\sqrt{4H(H+h)} \ \ \pm \ \ \sqrt{4H(H+h) - 4H(H+h)}}{-2(H+h)} \\ &= \sqrt{\frac{H}{H+h}} \\ &= \sqrt{\frac{1}{1+h/H}} \\ &= \sqrt{\frac{1}{1+2gh/v^2}} \\ \end{align*}\]

And hence finally we have

\[\boxed{\theta^* = tan^{-1}\sqrt{\frac{1}{1+2gh/v^2}}}\]

5. Further Problems

As we on the topic, let us discuss more about nature of the family of curve. Concretely, say you have a sprinklers tossing water uniformly at all angles in all direction (symmetry in 2D surface). Now what is the density of water w.r.t to radial distance from center. I.e there will be angles for which range doesn’t change much (spoiler: $\pi/4$), there water will log more compared to angles for which slight change results in greater range change. Let us try to model this problem -

We know $R = v^2sin2\theta/g$, ignore the constant for a while $R \sim sin2\theta$.

Little change in R, due to little nudge in $\theta$, is given by $dR = R^\prime(\theta)d\theta$, or $dR = \cos2\theta d\theta$. We ignored the constant again, you will see in a moment why we did so. We can frame our problem a bit mathematically by saying what we are looking for is the “measure” of logged water. Our measure is inversely proportional to $dR/d\theta$. As explained earlier, if a little nudge in angle leads to tail of water moving away less water is logged. One can understand this as for every point B on ground, for water to fall at B, there is a little window of $\theta$ for it. Actually 2 little windows near $\theta$ and $90^\circ - \theta$, but 2 is just constant so we don’t care. Now for B there are just these 2 points, but what we are talking about is what is the window length for points in proximity of B. I.e consider the region of say length $\Delta l$ around B, how big is the window for it? I.e how big is this interval $[\theta_{B-\Delta l}, \theta_{B+\Delta l}]$? We divide by $\Delta l$ just to remove it from our interval length as this is also a constant.

\[\mu_B \sim \Delta \theta \\\]

We know $\Delta l = cos2\theta \Delta \theta$, substituting in above and removing $\Delta l$ as it is just a constant we don’t care about -

\[\begin{align*} \mu_B &\sim \frac{\Delta l}{cos2\theta} \\ &= \frac{1}{cos2\theta} \\ &= \frac{1}{cos(sin^{-1}x_B/2H)} \\ \end{align*}\]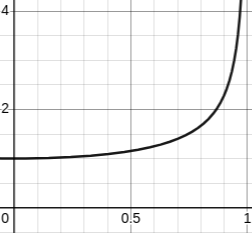

x-axis is $x_B/2H$ and y-axis is $\mu$

$x_B$ is the x-coordinate for point B. What $\mu_B$ indicate is the linear density of water logged, if you know about measure or pdf, probability density function, try thinking in terms of that. This will also clear how density can be infinite near $x_B = 2H$!. We removed all the constants as we are going to take care it now. Say total volume of water (or mass) fired through the hose is V. Note $\mu_B = 0$ for $x_B > 2H$.

\[\text{Vol} = k\int_l \mu_B dl \\\]

$\mu_B = 4H d\theta/dl$, using $dR = 2\cos2\theta (2H) d\theta$ (verify it once!).

\[\begin{align*} V &= k\int_0^{2H} \mu dl \\ &= k\int_{\theta(0)}^{\theta(2H)} 4H d\theta \\ &= k (4H\cdot \theta)|_0^{\pi/4} \\ &= k (H\pi) \\ \end{align*}\]

Giving $k = V/H\pi$. This is our normalization factor. Finally volume distribution (radially symmetry allows for no change! so our calculation holds same if sprinkler throws water $360^\circ$) around B is given by -

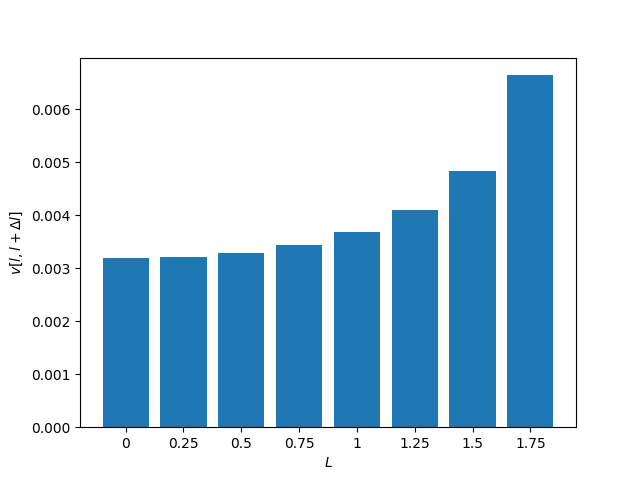
\[\begin{align*} v &= k\int_l^{l+\Delta l} \mu dl \\ &= k\int_{\theta(l)}^{\theta(l+\Delta l)} 4H d\theta \\ &= 4Hk (\theta)|_{sin^{-1}(l/2H)/2}^{sin^{-1}(l+\Delta l/2H)/2} \\ &= 2Hk \left(sin^{-1}\left(\frac{l+\Delta l}{2H}\right) - sin^{-1}\left(\frac{l}{2H}\right)\right) \\ &= \frac{V}{\pi} \left(sin^{-1}\left(\frac{l+\Delta l}{2H}\right) - sin^{-1}\left(\frac{l}{2H}\right)\right) \\ \end{align*}\]

Here $l = x_B$. Note is you put l = 0 and $\Delta l = 2H$, you get V as expected. Following is the plot for volume with H = 1, V = 1, dl = 0.01-

Plot only for selected points

For completion here is for all points (i.e “bars” slimmed to verticles lines) 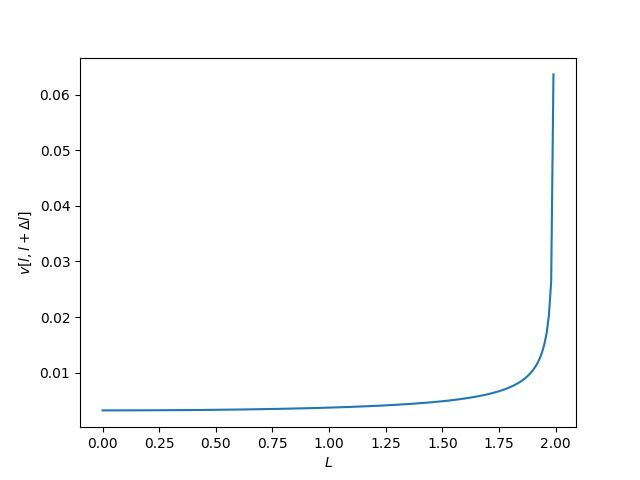For all points

6. Resources and Further Reading

1. IB Maths Resources
2. Stack overflow: Envelope of Projectile Trajectories
3. Envelope of Family of Angled Projectiles and Its Universal Geometric Characteristics by Haiduke Sarafian
4. On the Geometrical Approach to Projectile Motion by Philip Robinson
5. Wikipedia: Parabola of Safety
6. Butikov, E. I. (2003). Comment on The envelope of projectile trajectories . European Journal of Physics, 24(4), L5–L9. doi:10.1088/0143-0807/24/4/101
7. Mihas, P. (2019) Envelopes, Foci, and Maxima of Special Trajectories. American Journal of Physics, 87, 836.
8. No Calculus Needed?! How to Maximize Range Using Simple Geometry, YouTube Video by MathyJaphy
9. The Envelope of Projectile Trajectories, YouTube video by Elliot Nicholson
10. Stack overflow for maximum range and angle when launched from elevated surface

7. Footnotes

1. Technically car 2 had head start in time not in distance. But okayy! ↩︎